From Scratch: Writing a 3D Soft Engine 2/6

Now that we have built the core of our 3D engine along the lines of our previous tutorial #1, we will now work on enhancing the rendering. The next step is then to connect the dots to draw some lines in order to render what you probably know as a “wireframe” rendering. In today's tutorial, you will learn how to draw lines, what a face is and how cool is the Bresenham algorithm to draw some triangles.

Thanks to that, at the end, you will know how to code something as cool as that:

Yes! Our 3D rotating cube starts to really live on our screens!

First basic algorithm to draw a line between two points

Let’s start by coding a simple algorithm. To draw a line between 2 vertices, we’re going to use the following logic:

- if the distance between the 2 points (point0 & point1) is less than 2 pixels, there’s nothing to do 
- otherwise, we’re finding the middle point between both points (point0 coordinates + (point1 coordinates – point0 coordinates) / 2) 
- we’re drawing that point on screen 
- we’re launching this algorithm recursively between point0 & middle point and between middle point & point1

Here is the code to do that:

public void DrawLine(Vector2 point0, Vector2 point1)
   var dist = (point1 - point0).Length();
    // If the distance between the 2 points is less than 2 pixels
   // We're exiting
   if (dist < 2)
       return;
    // Find the middle point between first & second point
   Vector2 middlePoint = point0 + (point1 - point0)/2;
   // We draw this point on screen
   DrawPoint(middlePoint);
   // Recursive algorithm launched between first & middle point
   // and between middle & second point
   DrawLine(point0, middlePoint);
   DrawLine(middlePoint, point1);

public drawLine(point0: BABYLON.Vector2, point1: BABYLON.Vector2): void {
   var dist = point1.subtract(point0).length();
    // If the distance between the 2 points is less than 2 pixels
   // We're exiting
   if (dist < 2)
       return;
    // Find the middle point between first & second point
   var middlePoint = point0.add((point1.subtract(point0)).scale(0.5));
   // We draw this point on screen
   this.drawPoint(middlePoint);
   // Recursive algorithm launched between first & middle point
   // and between middle & second point
   this.drawLine(point0, middlePoint);
   this.drawLine(middlePoint, point1);

Device.prototype.drawLine = function (point0, point1) {
   var dist = point1.subtract(point0).length();
    // If the distance between the 2 points is less than 2 pixels
   // We're exiting
   if(dist < 2) {
       return;
   }
    // Find the middle point between first & second point
   var middlePoint = point0.add((point1.subtract(point0)).scale(0.5));
   // We draw this point on screen
   this.drawPoint(middlePoint);
   // Recursive algorithm launched between first & middle point
   // and between middle & second point
   this.drawLine(point0, middlePoint);
   this.drawLine(middlePoint, point1);
;

You need to update the rendering loop to use this new piece of code:

for (var i = 0; i < mesh.Vertices.Length - 1; i++)
   var point0 = Project(mesh.Vertices[i], transformMatrix);
   var point1 = Project(mesh.Vertices[i + 1], transformMatrix);
   DrawLine(point0, point1);

for (var i = 0; i < cMesh.Vertices.length -1; i++){
   var point0 = this.project(cMesh.Vertices[i], transformMatrix);
   var point1 = this.project(cMesh.Vertices[i + 1], transformMatrix);
   this.drawLine(point0, point1);

for (var i = 0; i < cMesh.Vertices.length -1; i++){
   var point0 = this.project(cMesh.Vertices[i], transformMatrix);
   var point1 = this.project(cMesh.Vertices[i + 1], transformMatrix);
   this.drawLine(point0, point1);

And you should now obtain something like that:

I know this looks weird but this was the expected behavior. It should help you starting to understand what you need to do to display a 3D mesh. But to have a better rendering, we need to discover a new concept.

Displaying faces with triangles

Now that we know how to draw lines, we need a better way to render the mesh with them. Thesimplest geometric 2D shape is a triangle. The idea in 3D is then to draw all our meshes by using those triangles. We then need to split each side of our cube into 2 triangles. We’re going to do this “manually” but we’ll see in the next tutorial that 3D modelers are doing this step automatically for us now.

To draw triangles, you need to have 3 points/vertices. A face is then simply a structure containing 3 values which are indexes pointing to the proper vertices array of the mesh to be rendered.

To be understand this concept, let’s take our previous figure with a Cube displayed by Blender:

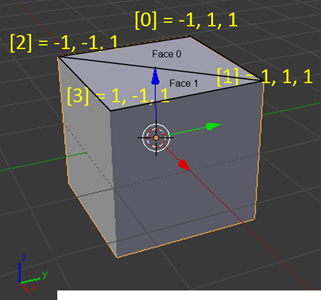
We have 4 vertices displayed on this figure with the following indices: 0, 1, 2, 3. To draw the upper side of the cube, we need to draw 2 triangles. The first one, Face 0, will be drawn with 3 lines from vertex 0(-1, 1, 1) to vertex 1 (1, 1, 1), from vertex 1 (1, 1, 1) to vertex 2 (-1, –1, 1) and finally from vertex 2 (-1, –1, 1) to vertex 0 (-1, 1, 1). The second triangle, Face 1, will be drawn with the lines from vertex 1 to vertex 2, vertex 2 to vertex 3 and vertex 3 to vertex 1.

The equivalent code would be something like that:

var mesh = new SoftEngine.Mesh("Square", 4, 2);
eshes.Add(mesh);
esh.Vertices[0] = new Vector3(-1, 1, 1);
esh.Vertices[1] = new Vector3(1, 1, 1);
esh.Vertices[2] = new Vector3(-1, -1, 1);
esh.Vertices[3] = new Vector3(1, -1, 1);
mesh.Faces[0] = new Face { A = 0, B = 1, C = 2 };
esh.Faces[1] = new Face { A = 1, B = 2, C = 3 };

If you want to draw to whole cube, you need to find the 10 remaining faces as we’ve got 12 faces for the 6 sides of our cube to draw.

Let’s now define the code for a Face object. It’s a very simple object as this is just a set of 3 indexes. Here’s the code of Face and the new Mesh definition which also now use it:

namespace SoftEngine
   public struct Face
   {
       public int A;
       public int B;
       public int C;
   }
   public class Mesh
   {
       public string Name { get; set; }
       public Vector3[] Vertices { get; private set; }
       public Face[] Faces { get; set; }
       public Vector3 Position { get; set; }
       public Vector3 Rotation { get; set; }
        public Mesh(string name, int verticesCount, int facesCount)
       {
           Vertices = new Vector3[verticesCount];
           Faces = new Face[facesCount];
           Name = name;
       }
   }

///
module SoftEngine {
   export interface Face {
       A: number;
       B: number;
       C: number;
   }
    export class Mesh {
       Position: BABYLON.Vector3;
       Rotation: BABYLON.Vector3;
       Vertices: BABYLON.Vector3[];
       Faces: Face[];
        constructor(public name: string, verticesCount: number, facesCount: number) {
           this.Vertices = new Array(verticesCount);
           this.Faces = new Array(facesCount);
           this.Rotation = new BABYLON.Vector3(0, 0, 0);
           this.Position = new BABYLON.Vector3(0, 0, 0);
       }
   }

var SoftEngine;
function (SoftEngine) {
   var Mesh = (function () {
       function Mesh(name, verticesCount, facesCount) {
           this.name = name;
           this.Vertices = new Array(verticesCount);
           this.Faces = new Array(facesCount);
           this.Rotation = new BABYLONTS.Vector3(0, 0, 0);
           this.Position = new BABYLONTS.Vector3(0, 0, 0);
       }
       return Mesh;
   })();
   SoftEngine.Mesh = Mesh;    
)(SoftEngine || (SoftEngine = {}));

We now need to update our Render() function/method of our Device object to iterate through all the faces defined and to draw the triangles associated.

foreach (var face in mesh.Faces)
   var vertexA = mesh.Vertices[face.A];
   var vertexB = mesh.Vertices[face.B];
   var vertexC = mesh.Vertices[face.C];
    var pixelA = Project(vertexA, transformMatrix);
   var pixelB = Project(vertexB, transformMatrix);
   var pixelC = Project(vertexC, transformMatrix);
    DrawLine(pixelA, pixelB);
   DrawLine(pixelB, pixelC);
   DrawLine(pixelC, pixelA);

for (var indexFaces = 0; indexFaces < cMesh.Faces.length; indexFaces++)
   var currentFace = cMesh.Faces[indexFaces];
   var vertexA = cMesh.Vertices[currentFace.A];
   var vertexB = cMesh.Vertices[currentFace.B];
   var vertexC = cMesh.Vertices[currentFace.C];
    var pixelA = this.project(vertexA, transformMatrix);
   var pixelB = this.project(vertexB, transformMatrix);
   var pixelC = this.project(vertexC, transformMatrix);
    this.drawLine(pixelA, pixelB);
   this.drawLine(pixelB, pixelC);
   this.drawLine(pixelC, pixelA);

for (var indexFaces = 0; indexFaces < cMesh.Faces.length; indexFaces++)
   var currentFace = cMesh.Faces[indexFaces];
   var vertexA = cMesh.Vertices[currentFace.A];
   var vertexB = cMesh.Vertices[currentFace.B];
   var vertexC = cMesh.Vertices[currentFace.C];
    var pixelA = this.project(vertexA, transformMatrix);
   var pixelB = this.project(vertexB, transformMatrix);
   var pixelC = this.project(vertexC, transformMatrix);
    this.drawLine(pixelA, pixelB);
   this.drawLine(pixelB, pixelC);
   this.drawLine(pixelC, pixelA);

We finally need to declare the mesh associated with our Cube properly with its 12 faces to make this new code working as expected.

Here is the new declaration:

var mesh = new SoftEngine.Mesh("Cube", 8, 12);
eshes.Add(mesh);
esh.Vertices[0] = new Vector3(-1, 1, 1);
esh.Vertices[1] = new Vector3(1, 1, 1);
esh.Vertices[2] = new Vector3(-1, -1, 1);
esh.Vertices[3] = new Vector3(1, -1, 1);
esh.Vertices[4] = new Vector3(-1, 1, -1);
esh.Vertices[5] = new Vector3(1, 1, -1);
esh.Vertices[6] = new Vector3(1, -1, -1);
esh.Vertices[7] = new Vector3(-1, -1, -1);
mesh.Faces[0] = new Face { A = 0, B = 1, C = 2 };
esh.Faces[1] = new Face { A = 1, B = 2, C = 3 };
esh.Faces[2] = new Face { A = 1, B = 3, C = 6 };
esh.Faces[3] = new Face { A = 1, B = 5, C = 6 };
esh.Faces[4] = new Face { A = 0, B = 1, C = 4 };
esh.Faces[5] = new Face { A = 1, B = 4, C = 5 };
mesh.Faces[6] = new Face { A = 2, B = 3, C = 7 };
esh.Faces[7] = new Face { A = 3, B = 6, C = 7 };
esh.Faces[8] = new Face { A = 0, B = 2, C = 7 };
esh.Faces[9] = new Face { A = 0, B = 4, C = 7 };
esh.Faces[10] = new Face { A = 4, B = 5, C = 6 };
esh.Faces[11] = new Face { A = 4, B = 6, C = 7 };

var mesh = new SoftEngine.Mesh("Cube", 8, 12);
eshes.push(mesh);
esh.Vertices[0] = new BABYLON.Vector3(-1, 1, 1);
esh.Vertices[1] = new BABYLON.Vector3(1, 1, 1);
esh.Vertices[2] = new BABYLON.Vector3(-1, -1, 1);
esh.Vertices[3] = new BABYLON.Vector3(1, -1, 1);
esh.Vertices[4] = new BABYLON.Vector3(-1, 1, -1);
esh.Vertices[5] = new BABYLON.Vector3(1, 1, -1);
esh.Vertices[6] = new BABYLON.Vector3(1, -1, -1);
esh.Vertices[7] = new BABYLON.Vector3(-1, -1, -1);
mesh.Faces[0] = { A:0, B:1, C:2 };
esh.Faces[1] = { A:1, B:2, C:3 };
esh.Faces[2] = { A:1, B:3, C:6 };
esh.Faces[3] = { A:1, B:5, C:6 };
esh.Faces[4] = { A:0, B:1, C:4 };
esh.Faces[5] = { A:1, B:4, C:5 };
mesh.Faces[6] = { A:2, B:3, C:7 };
esh.Faces[7] = { A:3, B:6, C:7 };
esh.Faces[8] = { A:0, B:2, C:7 };
esh.Faces[9] = { A:0, B:4, C:7 };
esh.Faces[10] = { A:4, B:5, C:6 };
esh.Faces[11] = { A:4, B:6, C:7 };

var mesh = new SoftEngine.Mesh("Cube", 8, 12);
eshes.push(mesh);
esh.Vertices[0] = new BABYLON.Vector3(-1, 1, 1);
esh.Vertices[1] = new BABYLON.Vector3(1, 1, 1);
esh.Vertices[2] = new BABYLON.Vector3(-1, -1, 1);
esh.Vertices[3] = new BABYLON.Vector3(1, -1, 1);
esh.Vertices[4] = new BABYLON.Vector3(-1, 1, -1);
esh.Vertices[5] = new BABYLON.Vector3(1, 1, -1);
esh.Vertices[6] = new BABYLON.Vector3(1, -1, -1);
esh.Vertices[7] = new BABYLON.Vector3(-1, -1, -1);
mesh.Faces[0] = { A:0, B:1, C:2 };
esh.Faces[1] = { A:1, B:2, C:3 };
esh.Faces[2] = { A:1, B:3, C:6 };
esh.Faces[3] = { A:1, B:5, C:6 };
esh.Faces[4] = { A:0, B:1, C:4 };
esh.Faces[5] = { A:1, B:4, C:5 };
mesh.Faces[6] = { A:2, B:3, C:7 };
esh.Faces[7] = { A:3, B:6, C:7 };
esh.Faces[8] = { A:0, B:2, C:7 };
esh.Faces[9] = { A:0, B:4, C:7 };
esh.Faces[10] = { A:4, B:5, C:6 };
esh.Faces[11] = { A:4, B:6, C:7 };

You should now have this beautiful rotating cube:

Congrats! :)

Enhancing the line drawing algorithm with Bresenham

There is an optimized way to draw our lines using the Bresenham’s line algorithm. It’s faster & sharper than our current simple recursive version. The story of this algorithm is fascinating. Please read the Wikipedia definition of this algorithm to discover how Bresenham build it and for which reasons.

Here are the versions of this algorithm in C#, TypeScript and JavaScript:

public void DrawBline(Vector2 point0, Vector2 point1)
   int x0 = (int)point0.X;
   int y0 = (int)point0.Y;
   int x1 = (int)point1.X;
   int y1 = (int)point1.Y;
           
   var dx = Math.Abs(x1 - x0);
   var dy = Math.Abs(y1 - y0);
   var sx = (x0 < x1) ? 1 : -1;
   var sy = (y0 < y1) ? 1 : -1;
   var err = dx - dy;
    while (true) {
       DrawPoint(new Vector2(x0, y0));
        if ((x0 == x1) && (y0 == y1)) break;
       var e2 = 2 * err;
       if (e2 > -dy) { err -= dy; x0 += sx; }
       if (e2 < dx) { err += dx; y0 += sy; }
   }

public drawBline(point0: BABYLON.Vector2, point1: BABYLON.Vector2): void {
   var x0 = point0.x >> 0;
   var y0 = point0.y >> 0;
   var x1 = point1.x >> 0;
   var y1 = point1.y >> 0;
   var dx = Math.abs(x1 - x0);
   var dy = Math.abs(y1 - y0);
   var sx = (x0 < x1) ? 1 : -1;
   var sy = (y0 < y1) ? 1 : -1;
   var err = dx - dy;
    while (true) {
       this.drawPoint(new BABYLON.Vector2(x0, y0));
        if ((x0 == x1) && (y0 == y1)) break;
       var e2 = 2 * err;
       if (e2 > -dy) { err -= dy; x0 += sx; }
       if (e2 < dx) { err += dx; y0 += sy; }
   }

Device.prototype.drawBline = function (point0, point1) {
   var x0 = point0.x >> 0;
   var y0 = point0.y >> 0;
   var x1 = point1.x >> 0;
   var y1 = point1.y >> 0;
   var dx = Math.abs(x1 - x0);
   var dy = Math.abs(y1 - y0);
   var sx = (x0 < x1) ? 1 : -1;
   var sy = (y0 < y1) ? 1 : -1;
   var err = dx - dy;
   while(true) {
       this.drawPoint(new BABYLON.Vector2(x0, y0));
       if((x0 == x1) && (y0 == y1)) break;
       var e2 = 2 * err;
       if(e2 > -dy) { err -= dy; x0 += sx; }
       if(e2 < dx) { err += dx; y0 += sy; }
   }
;

In the render function, replace the call do DrawLine by DrawBline and you should notice that this is a bit more fluid & a bit more sharp:

If you’re observing it with attention, you should see that this version using Bresenham is less choppy than our first algorithm.

Again, you can download the solutions containing the source code:

– C# : SoftEngineCSharpPart2.zip

- TypeScript : SoftEngineTSPart2.zip

- JavaScript : SoftEngineJSPart2.zip or simply right-click –> view source on the embedded iframe

In our next tutorial, you will learn how to export some Meshes from Blender, a free 3D modeler tool, into a JSON format. We will then load this JSON file to display it with our wireframe engine. Indeed, we already have everything setup to display much more complex meshes like these one:

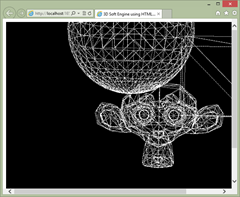
See you in the third part of this series.

About the Author

David Rousset is a Developer Evangelist at Microsoft, specializing in HTML5 and web development. Read his blog on MSDN or follow him @davrous on Twitter.

(dpe)